 |
Как игроку максимизировать выигрыш в игровых автоматах? Эта проблема вдохновляет на решение проблемы многорукого бандита — распространенной задачи обучения с подкреплением, в которой агенты делают выбор, чтобы получить вознаграждение. Недавно международная исследовательская группа под руководством Хироаки Синкавы из Токийского университета разработала расширенную схему фотонного обучения с подкреплением, которая позволяет перейти от статичной задачи о бандите к более сложной динамической среде. Исследование опубликовано 25 июля в журнале Intelligent Computing, a Science Partner Journal. Успех схемы зависит как от фотонной системы, повышающей качество обучения, так и от поддерживающего алгоритма. Рассматривая «потенциальную фотонную реализацию», авторы разработали модифицированный алгоритм бандитского Q-обучения и подтвердили его эффективность с помощью численного моделирования. Они также протестировали свой алгоритм в параллельной архитектуре, где несколько агентов работают одновременно, и обнаружили, что ключом к ускорению параллельного процесса обучения является предотвращение конфликтующих решений за счет использования квантовой интерференции фотонов. Хотя использование квантовой интерференции фотонов не является
В данном исследовании рассматривается сетчатый мир, представляющий собой набор ячеек с различным вознаграждением. Каждый агент может двигаться вверх, вниз, влево или вправо и получать вознаграждение в зависимости от своего текущего перемещения и местоположения. В этой среде следующий ход агента полностью определяется его текущим ходом и местоположением. При моделировании в данном исследовании используется сетка 5 × 5 ячеек; каждая ячейка называется «состоянием», каждое движение, совершаемое агентом на каждом временном шаге, называется „действием“, а правило, определяющее, как агент выбирает то или иное действие в каждом состоянии, называется „политикой“. Процесс принятия решений строится как сценарий задачи бандита, где каждая пара „состояние — действие“ рассматривается как игровой автомат, а изменения величины Q — значений пар „состояние — действие“ — считаются вознаграждением. В отличие от базовых алгоритмов Q-обучения, которые обычно сосредоточены на поиске оптимального пути для максимизации вознаграждения, модифицированный бандитский алгоритм Q-обучения нацелен на эффективное и точное обучение оптимальному значению Q для каждой пары «состояние-действие» во всей среде. Поэтому агенту необходимо соблюдать баланс между „эксплуатацией“ знакомых пар с высокими значениями для ускорения обучения и „исследованием“ нечасто встречающихся пар для получения потенциально более высоких значений. В качестве политики используется алгоритм softmax — популярная модель, которая отлично справляется с подобным балансированием. Первоочередной задачей авторов является разработка фотонной системы, поддерживающей бесконфликтное принятие решений как минимум тремя агентами, в надежде, что ее добавление в предложенную ими схему поможет агентам избежать принятия противоречивых решений. В то же время они планируют разработать алгоритмы, позволяющие агентам действовать непрерывно, и применить свой алгоритм бандитского Q-обучения к более сложным задачам обучения с подкреплением. 21.08.2023 |
Net&IT
 | |
| ИИ-платформа для анализа изображений поможет развивать исследования во всем мире | |
Группа исследователей из Института Гульбе... | |
 | |
| Инженеры воссоздали голопалубу Star Trek с помощью ChatGPT и видеоигр | |
В сериале Звездный путь: Следующее поколение к... | |
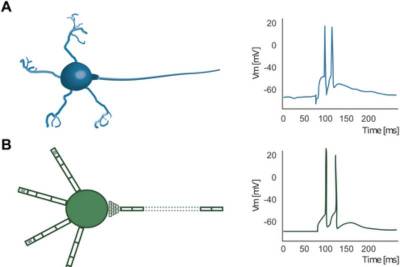 | |
| IC: Исследователи тестируют биологическую безвредность нейроморфной сети | |
Биологический мозг, в особенности человеч... | |
 | |
| Science: Аналоговые вычисления дают решать сложные уравнения и экономят энергию | |
Группа исследователей, включая инженеров Масса... | |
 | |
| В 40% случаев люди ошибочно называют сгенерированное фото человека реальным | |
Если вам недавно было трудно понять, явля... | |
 | |
| Physical Review X: Сеть квантовых датчиков повышает точность измерений | |
Квантовые системы, используемые в квантов... | |
 | |
| Scientific Reports: ИИ показал больший творческий потенциал, чем человек | |
Еще один балл в пользу искусственного инт... | |
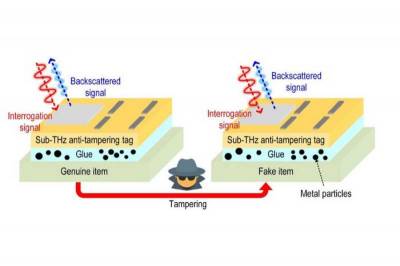 | |
| Крошечную метку на замену RFID сделали еще надежнее | |
Несколько лет назад исследователи Массачу... | |
 | |
| Привыкнув доверять, люди не поймут, когда ИИ начнет манипулировать | |
Согласно обширному обзору, в настоящее вр... | |
 | |
| Умные серьги с низким энергопотреблением будут измерять температуру по мочке уха | |
Умные аксессуары становятся все более рас... | |
 | |
| Для борьбы с бешенством разработали приложение для распознавания собачьих морд | |
Новое приложение для распознавания собачь... | |
 | |
| Генеративный ИИ помогает ученым объяснить человеческую память и воображение | |
Последние достижения в области генеративн... | |
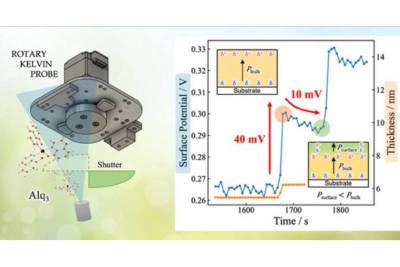 | |
| Ученые приблизились к более легким и гибким оптоэлектронным устройствам | |
Органические оптоэлектронные устройства, такие... | |
 | |
| ChatGPT перелопатил почти весь интернет, но пока не научился рассуждать | |
Языковые модели ИИ переживают бум. В ... | |
 | |
| Если сотрудникам скорой помощи поможет ИИ, они смогут спасать больше жизней | |
Чтобы определить, насколько серьезно пострадал... | |
 | |
| Беспроводная система отслеживания улучшит впечатления от расширенной реальности | |
Новая технология, разработанная инженерами Кал... | |
 | |
| PNAS Nexus: ИИ пока еще далеко до человеческих способностей мыслить | |
Атанасиос С. Фокас рассматривает актуальный во... | |
 | |
| Nature: ИИ генерирует белки с исключительной прочностью связывания | |
В новом исследовании, опубликованном 18 декабр... | |
 | |
| Nature Computational Science: ИИ может предсказывать события в жизни людей | |
Искусственный интеллект, разработанный для&nbs... | |
 | |
| Разработан фреймворк ИИ для определения новых показаний к применению лекарств | |
Ученые из компании Klick Applied Sciences... | |
 | |
| Искусственный интеллект отлично справляется с имитацией, но не с инновациями | |
Системы искусственного интеллекта часто изобра... | |
 | |
| Nature Electronics: Изменение памяти дает новые вычислительные возможности | |
Ученые Рочестерского университета разработали ... | |
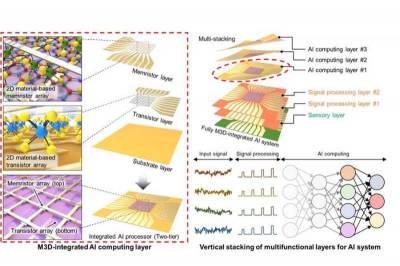 | |
| Nature: 2D-материал изменяет форму 3D-электроники для искусственного интеллекта | |
Многофункциональные компьютерные чипы эволюцио... | |
 | |
| Началась регистрация на конкурс «Битва искусственных интеллектов» | |
Стартовал отборочный этап Международного техно... | |
 | |
| Наступает новая эра творческого партнерства в эпоху генеративного ИИ | |
Последние достижения в области генеративн... | |
 | |
| Ученые разрабатывают инструменты для использования ИИ в юридическом образовании | |
В то время как многие с опаской... | |
 | |
| Создан метод тонкой настройки модели ИИ на устройствах с ограниченными ресурсами | |
Персонализированные модели глубокого обучения ... | |
 | |
| Новая уязвимость процессора подвергает опасности виртуальные машины | |
В области облачных вычислений, то есть до... | |
 | |
| Разработан новый квантовый подход к безопасности облачных хранилищ данных | |
Распределенные облачные хранилища —... | |
 | |
| ACS Applied Energy Materials: Разработаны солнечные батареи для помещений | |
Так называемый Интернет вещей — от&... | |
